编者按:从孪生素数到梅森素数,从狄利克莱定理到阿廷猜想,从瓦格斯塔夫素数到斐波那契素数,从简单的多项式到到复杂的指数式,人类对素数的探索一直没有停止过。今天我们欣喜地看到,此次思想探险仿佛征服了那冷傲的雪山,它象春雨般无声地润泽万物,惠及百科而不自知。神秘布局素数的幕后推手终于露脸了,原来它就是二维素数基底。没有端则没有类,有类则有端,二元互补区分中,端和类是同构的,多元并置区分中,端和类是同态的。二元的始终与内外是同构的,多元的过去现在未来与上中下则是同态的。法不传六耳,推动数学发展的引擎原来就是相邻思想。
【摘要】 无限递增的二维线性空间必有无限递增的二维素数基底的思想是笔者用来证明考拉兹猜想、哥德巴赫猜想成立的重要数学工具,用它再结合哥德巴赫猜想、孪生素数猜想、波利尼亚克猜想已经获证的结论,以及费马小定理和洛书定理,可成功证明梅森素数猜想以及斐波那契素数猜想成立。由此可窥见指数式以及递归式表达的大素数的某些分布规律。
【关键词】 梅森素数猜想;梅森数;斐波那契素数猜想;斐波那契数,二维素数基底,洛书定理;哥德巴赫猜想;相邻论;费马螺线素数模型;邻函数恒等式;狄利克莱定理;波利尼亚克猜想;斋藤猜想;费马小定理。

黄金分割律表现在宇宙构造中
我们知道带数值和字母运算的通项式表达和递归式表达大致可分为,初等解析式与非初等解析式。其中初等解析式包括运算次数有限的初等代数式和初等超越式,而初等代数式又包括单项式,多项式,分式和指数式、根式,初等超越式则包括无理数指数式、对数式、三角函数式、反三角函数式、双曲函数式、幂指函数式等。非初等解析式主要包括运算次数无穷的代数式和超越式,用这些解析式来表达的素数是否无穷证明起来无疑会更加艰难。
作者在《数学底层引擎相邻论和重合法》完成证明过不可约多项式可表无穷素数,澎湃新闻发布过《任意给定的整系数不可约多项式 f(x)皆可表无穷素数》一文,但更复杂的解析式是否也能表达无穷素数呢?作者在新书专集里发表过,还有几类素数也是无穷的。本文就来尝试证明,指数式表达的斐波那契素数有无穷多个,指数式表达的梅森素数有无穷多个,这两类素数表达不属于多项式可刻画的范畴,属于指数式,证明起来难度更大。形如2^p-1型素数为梅森素数,形如1/√5{(1+√5)^n/2^n-(1-√5)^n/2^n}为斐波那契素数,这两类素数都是指数式的,后者甚至是无限迭代型的。那这两种类型素数是否也无穷呢?数学界十分关注。
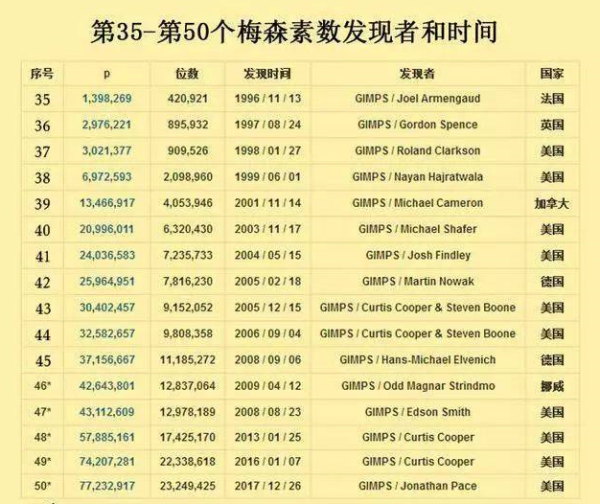
梅森素数第1到第50个
1. 借助费马小定理,证明梅森素数猜想
梅森数是指形如 2^p-1 的正整数,其中指数 p 是素数,常记为 Mp。若 Mp 是素数,则称为梅森素数①(Mersenne Prime)。p=2,3,5,7 时,Mp 都是素数,但 M11=2047=23×89 不是素数 ,是否有无穷多个梅森素数是数论中未解决的难题之一。截至 2013 年 2 月累积发现 48 个梅森素数,Mp =2^57885161-1,此时 Mp是一个 17425170 位数。这项发现雄冠了 3 年,但在 2016 年的第一个星期,美国密苏里中央大学数学家柯蒂斯 • 库珀(Curtis Cooper)发现了第 49 个“梅森素数”。该素数“2 的 74207281 次方减 1”,有 2200 多万位,如果用普通字号打印出来,长度将超过 65 公里。后又发现了第50个梅森素数,2^77232917-1。
梅森素数是否有无穷个?从目前了解到的例证看,非常稀少,但总可不断发现新的梅森素数,梅森素数是否无穷尚未有可直观理解的判定,它需要一个纯数学证明。以下是最简洁的关于梅森素数猜想的纯数学证明。
如果梅森数(2^p-1)≡ 1mod(Mp),即 2^p ≡ 2 mod(Mp)。
另根据哥德巴赫猜想获证,必有新素数(p+2n)存在。
则 2^(p+2n)≡ 2^(2n+1) mod(Mp)。
2^(2n+1)是指数为奇数的密集 2 幂数(即 2 的任意次幂)偶数,故可取
2(2n+1)=Mp+1,则{2^(p+2n)-1}≡ 0 mod(Mp )。
故有梅森素数 Mp 存在。
如果梅森数(2^p-1)≡ 2mod(Mp ),即 2^p ≡ 3 mod(Mp )。
另根据哥德巴赫猜想获证,必有新素数(p+2n)存在。
则 2^(p+2n)≡ 3×2^2n mod(Mp )。
3×2^2n 也是偶数,可取 2^(2n+1)=Mp+1,
那么 3×2^2n=2^2n+2^(2n+1)=Mp-1,则{2^(p+2n)-1}≡ 2^2n mod(Mp),
在此基础上再取新素数所对应的梅森数,得:
2^(p+2n)≡ 2^(2n+1)2^(2n+1) mod(Mp ) 2^(2n+1) 是指数为奇数的密集 2 幂数偶数,故可取 2^(2n+1)=Mp+1,则{2^(p+2n)-1}≡ 0 mod(Mp )。
故有梅森素数 Mp 存在。
如果梅森数(2^p-1)≡ 3mod(Mp ),即 2^p ≡ 4 mod(Mp )。
另根据哥德巴赫猜想获证,必有新素数(p+2n)存在。
则 2^(p+2n)≡ 2^(2n+1)+2^(2n+1) mod(Mp )。
2^(2n+1) 是指数为奇数的所有 2 的幂级数偶数,故可取 2^(2n+1)=Mp+1,
则{2^(p+2n)-1}≡ 0 mod(Mp )。
故有梅森素数 Mp 存在。
……
现假设:如果梅森数(2^p-1)≡ 2^x-1 mod(Mp ),即 2^p ≡ 2x mod(Mp )
另根据哥德巴赫猜想获证,必有新素数(p+2n)存在。
则 2^(p+2n)≡ 2^(2n+1) mod(Mp )。
2^(2n+1) 是指数为奇数的密集 2 幂数偶数,故可取 2^(2n+1)=Mp+1,
则{2^(p+2n)-1}≡ 0 mod(Mp )。
故有梅森素数 Mp 存在。
如果梅森数(2^p-1)≡ 2x mod(Mp ),即 2^p ≡ 2x+1 mod(Mp )。
另根据哥德巴赫猜想获证,必有新素数(p+2n)存在。
则 2^(p+2n)≡ 2^(2n)+x2^(2n+1) mod(Mp )。
2^(2n+1) 是指数为奇数的密集 2 的幂级数偶数,故可取 2^(2n+1)=Mp+1,
则{2^(p+2n)-1}≡ 2^(2n) mod(Mp )。
在此基础上再取新素数所对应的梅森数,得:
2^(p+2n)≡ 2^(2n+1)2^(2n+1) mod(Mp ), 2^(2n+1) 是指数为奇数的密集 2 的幂级数偶数,故可取 2^(2n+1)=Mp+1,
则{2^(p+2n)-1}≡ 0 mod(Mp )。
故有梅森素数 Mp 存在。
所以从余数 1 到余数 Mp-1,无论是奇数还是偶数,即:
梅森数 2^p-1 除以梅森素数 Mp 所得到的所有余数,都可以通过梅森数 2^p-1
中的指数 p 递增偶数 2n 差值而获得新素数 p;
而此时的新 p 指数所对应的梅森数整除 Mp 时,定可得到商数为 1 余数为 0,即:{2^(p+2n)-1}= Mp
由于根据哥猜获证的结论(p+2n)可得到无穷无漏的新素数,故凭此也可得到无穷无漏的新梅森素数。于是梅森素数猜想获证。之所以梅森素数猜想能够获证,是因为指数密集递增与同余数周期递增之间存在交集,由此可捕捉整系数多项式的性态。
以上为简洁证明。

黄金分割律表现在艺术创作中
2. 根据相邻论,证明梅森素数猜想
此外,还可以用其他方法来证明。现我们假设梅森素数是有限的,最后一个梅森素数为 Mp,那么大于 Mp 的 p 为任意素数(p < Mp),即 2^p-1 就是一个奇合数。比有限数 Mp 大的 2^k-1 真的一定都是合数吗?
大于 Mp 的梅森素数 Mk 与最大梅森素数 Mp 的差是 2^k-1-Mk,而这个值属于偶数范围,只要素数无限延伸就存在任意的偶数差,因为斋藤猜想被证明,已显示了这一点,因此在最大梅森素数 Mp 的基础上无限延伸素数,必可以通过一个偶数差获得新素数,很多新偶数共轭素数对,都可以变换为共轭差最大的素数对,其中最小奇素数为 3,而这个偶数差同 2^k-1-Mp 若定有交集,梅森素数就会再次出现。这就会与之前假设比有限数 Mp 大的 2^k-1 一定是奇合数相矛盾。现在来证明偶数最大素数共轭差与梅森数减 3 或减较小素数一定会有交集。
假如 2^p-1 为有界素数,那么 p 就是一个有界素数,即等价于假设大于指数p 的梅森数将不存在素数。若 2^k-1 为非素数,那么 2^k-1 就是一个奇合数,根据洛书定理,所有的奇数都可表达成 2^k-1 以及 2k 的偶数补集 +1,即由 2^k 得 到 2n-(2^k-1),既然大于 2^p-1 的素数不在(2^k-1)中,那么就应该全部都在 2n- (2^k-1)中,由此可知大于 2^p-1 的所有梅森素数都是通过 2n 偶数减去梅森数所得到的。也可表达成 |2^p-1-2n|,它是所有奇数 |2^k+1+2n| 的一个子集。
大于 2^p-1 的梅森素数 Mk 的所有大素数都可以通过偶数减去梅森数 2^n- 2^k+1 得到,以梅森数为中值的共轭差最小互质素数有且只有一对,不小于 8 的偶数都有一对这样的共轭差最小的互质素数,这是哥德巴赫猜想所证明过的结论。当共轭差为 0 时,梅森数就是梅森素数了。
由于大于 2^p-1 的梅森数不是素数,也不含素数,所以就不能得到 2n-(2^p-1)同时又是素数的奇数(2^p-1),由于 k>p,则(2^k-1)>(2^^p-1)有无穷组,2^n-(2^k-1)也有无穷组。
因为 2^k-1=Mk,所以 2^k+2=Mk+3,根据相邻论,无论是 2^p 的相邻偶数还是2^p 的相邻偶数,经过有限项的偶数递增后,必封顶,不能通过小于给定数的素数两两相加获得。此时必有新增素数参与才能获得,而 2^k+2 是一个偶数相邻递增数,因此每每经过有限项的偶数递增都需要新增的 Mp 才能相加获得。因此不允许梅森数持续后继列举都不是素数,除非 Mk-3 同 2^k-4 永远没有交集,或 Mk-p 小同 2^k-p 小 -1 永远没有交集,偶数 2^k-4 都是 Mk 与非 3 素数相减获得的。
若那样就加不出新偶数。而根据相邻论,必有新素数参与才能获得新增相邻偶数。若匹配的梅森素数有限,那么 2^p+2 必有限,即 p 为有限素数,但我们已知,素数是无穷的,2^p+2 也是无穷的,因此 Mp 也必是无穷的。根据哥德巴赫猜想相邻论法则:
2^p 的相邻偶数 2^p+2 必须由大于 p 的素数与小素数组合才能获取。2^p的相邻偶数2p+2同样必须由大于某素数的素数与小素数组合才能获取。较大素数 p 大 +3-2 即素数加 3 的递减相邻偶数,必不能用 p 大及其域内素数相加获得,而是要用递减相邻素数及其域内素数相加才能获得。

第50个梅森素数
3. 根据斋藤定理,也能证明梅森素数猜想
有梅森素数方程 2^p-1=Mp,经变换得 2^p-4=Mp-3,先要证明 Mp 是无穷数,根据斋藤定理可知道,差值等于 2n 的素数对是存在的,只有 Mp 为无穷素数时才能办到。2^p-4 则是一个偶数集,该偶数集的递增带来了新素数的递增,根据哥德巴赫猜想的两素数定理,偶数值的表达可以替换为两个共轭差值最大的两素数表示,由于最小的奇素数为 3,Mp 为新增素数。
梅森数 2^p-1 不可能仅仅是素数,因为根据波利尼亚克定理②可以知道,任意差值的素数对都各有无穷组。从素数 p 到梅森素数 2^p-1 相差一个很大的偶数值,但无论这个偶数值有多大,都有一个偶数值匹配,因为任意差值的素数对都存在。与 p 构成素数对的那个数与梅森数的公差恰好一致,此时梅森数就是梅森素数。
梅森数的 2 倍加 2 所获得的偶数必须有新增素数参加才能获得。当无法用给定内的素数相加获得时,梅森数就必须是梅森素数。
当 2Mp 不能用 Mp 以内的两素数表达的时候,2Mp 就一定跟梅森素数相关,随着梅森数的指数不同,会反复出现这样的周期,用给定数内两素数相加获得梅森数2倍的相邻偶数从强到弱,弱到不能产生,此时梅森数就一定是梅森素数。
从而组合因变量新偶数的能力又变强,由此进入下一轮,直到山穷水尽不能再组合得到新的因变量新偶数,迫使自变量选下一个相邻值,此时梅森数就一定是梅森素数,如此周而复始,不断处于这样的反复迭代运算中。从而判定梅森素数是无穷的。
大凡证明无穷性的问题,都是因为存在某种趋于无穷的通项运算,且这种无穷通项运算是开放的。梅森素数就是这样。梅森素数是分布在奇数集合中的无限域,它有指数式通项表达 2^p-1,它由无穷素数所确定,同时它又需要无穷素数来排除筛选掉不是素数的梅森数,具有筛选能力的素数群是可确定的,可给定的,虽然它们的筛选能力是有界的,但可以产生新成果,于是将新成果纳入筛选工具中,又进一步进行筛选,获得更新的成果,此过程不断通项连续进行。这就是梅森数为什么到后继延伸到一定的时候非得是素数不可的原因。
这与欧几里得证明素数的无穷性是很相似的。他是通过构造新素数,无法被旧素数囊括,从而证明该类素数具无穷性的。在这里也是如此,梅森数核心配件无法通过小于该指数的素数对相加获得,从而反证出梅森素数是无穷的。

素数世界扑簌迷离
4. 任意类型的无穷素数不可通项表达定理
其实任何通项式经过或加 1 或减 1 或加 2 或减 2 形成不可分解多项式都可以获得新素数,且能无穷获得新素数。但任何通项式经过或加 1 或减 1 或加 2或减 2 所形成的多项式都不能得到全部素数,素数是不可通项表达的。这是把孪生素数猜想、梅森素数猜想变为一般化的猜想表达。
全集素数不可通项表达,类型素数也不可通项表达:自然数不能完全用素数为自变量进行通项式表达,自然数可以用素数为自变量进行相邻迭代式表达;
素数不能完全用自然数为自变量进行通项式表达,素数可以用自然数为自变量进行相邻迭代式表达。素数某类无穷子集不可用自然数或素数为自变量进行通项表达,除非混含另类,如费马素数表达式会混含费马数。
以上判定看似比孪生素数猜想更广义,更一般化,其实它是孪生素数猜想成立后的推论,这是不是有点反直觉?正如波利尼亚克猜想是孪生素数猜想的推论一样,以上判定也是孪生素数猜想的推论。孪生素数猜想成立,故差值为2n 的素数对是无穷的也就成立。既然差值 2n 的素数对是无穷的,那么就可用素数为自变量构造出任意通项式表达。用差值 2 进行切割和连接可以得到所有偶数,波利尼亚克猜想正是这样证明的,于是差值 2n 的无穷素数对就获得了证明,其中 2n 通过除以 2 可还原获得所有自然数,于是素数无穷子集都可以在任意差值中找到对应通项式。
梅森素数通项式也不例外,因为差值 2n 的素数对都是无穷的。差值 2n 的奇数对虽然也是无穷的,但包含素数中的一个无穷子集。同样无穷奇数包含差值 2 ∧ p2-2 ∧ p1 的无穷梅森数,如果无穷梅森数仅仅包含有穷梅森素数,将导致很多新的梅森数无法产生。两个梅森素数之间的差值等于 2^p2-2^p1。可以看出2^p2-2^p1 是一个偶数,只不过这个偶数是变化的,不是一个常数。但是就算变化,也全部都在 2n 的偶数集中,每次是可偶数给定的。以下进入关键证明:
偶数与奇数的相邻差值为 1,合数与奇数的相邻差值有时为 1 有时为 2。根据洛书定理可变换推理得到,偶数可表示为 |2^p-2k|(p 为素数,2k 为偶数,它与 2a+2^n 是等价表达),再根据哥德巴赫猜想两素数原理,偶数集 |2^p-2k| 可变换为 |2^p-1+p|(当 p 为素数时)或 |2^p-1+t|(当 2^p-1 不是素数,t 为奇合数时)。
由此表达式可知,当 2k 的相邻数为素数时,一定存在素数可以用 2^p-1 表示,当 2k 的相邻数为奇合数时,也一定存在奇合数可以用 2^p-1 表示。
k 任意足够大时,仍一直存在 2k 的相邻数或为奇数或为素数。若 2^k 为有限数,大于 2^k 的偶数,其相邻数不可能永远都是奇合数,当中定有素数,因此就会对应得到 2^p-1 为梅森素数。任意设置给定数,都能找到大于 2^k 的偶数,其相邻数不可能永远都是奇合数,当中定有素数。因为自然数的延伸,素数是无穷的,奇合数也是无穷的,它们交替重现,新素数会筛选掉合数,当新素数不增长时,筛选合数的能力会到尽头或者有漏项,此时必须新增素数,否则自然数不能密集延伸。一旦有了新增素数,构造合数的能力随即加强,于是合数又不断出现,直到组合出现尽头,又有新素数出现。
欧几里得已经证明了素数与奇合数、偶合数会无穷交替延伸。而梅森数正是奇数的其中一个无穷子集,里头的素数与奇合数也同样是反复交替出现的。
|2^p-1+p|(当 p 为素数时)或 |2^p-1+t|(当 t 为奇合数时),可得到偶数全集。根据假设得知,大于给定数的(2^p-1)都是奇合数,故一定能分解。因为 t 为奇合数,还因为这里的密集 t 是 2n-(2^p-1)所得到,所以这里的2p-1 也是奇合数;因为 p 为素数,还因为这里的密集 p 是 2n-(2^p-1)所得到,所以这里的2^p-1 也为素数。
当偶数是 2^p-1 的 2 倍时,要得到密集素数时,须 2p-p 获得 p,要获得密集奇合数时,须 2t-t 获得 t,否则偶数集就是有漏的。因此既然要获得无漏的偶数集合,就定要选择 |2^p-1+p|,且 2^p-1= p,才会无漏。这就与大于给定数的(2^p-1)都是奇合数相矛盾。
可见假定大于给定数的(2^p-1)都是奇合数就是错误的,必须允许梅森数反复出现梅森素数,因为无论该给定数设置多大,都会出现这样的逻辑悖论,因此梅森素数必须是无穷的。
当年欧几里得证明素数无穷性的方法,同样可以用于证明各种通项表达的特殊类素数的无穷性判定。欧几里得是通过素数若有穷,则可以构造一个新数,无法用所有的有穷素数整除,从而反证出这个新数一定是素数,以此说明素数是无穷的。怀海德(Whitehead)说:“纯数学这门科学在其现代发展阶段,可以说是人类精神之最具独创性的创造。”因为每一次创新,都要依赖已有的全部发现。
同样,各种通项表达的特殊类素数若有限,则可以同样构造一个用该通项表达的特殊类新数,无法用所有的有穷素数整除,或无法用所有的无穷但有漏素数整除,从而反证出这个新数一定是素数,以此说明该类素数是无穷无漏的。
新梅森素数猜想就是该类猜想的一个推广,也叫阿廷猜想。这个猜想同二次互反律相关,因此阿廷猜想也是二次互反律的推广, 对于任意不等于 1,p-1及完全平方的正整数 a,必存在无穷多个素数 p,以 a 为原根。这一猜想被称为阿廷猜想,至今尚未解决。而朗兰兹纲领就是以阿廷猜想为起点的进一步推广。因此阿廷猜想极为重要,新梅森素数猜想是这样表达的:
对于任何奇自然数 p,若以下其中两句叙述成立,剩下的一句就会成立:
1. p=(2^k)±1 或 p=(4^k)±3 是无穷质数(含阿廷猜想);
2.(2^p)-1是无穷质数(梅森质数);
3.[(2^p)+1]/3 是无穷质数(瓦格斯塔夫质数)。
这三句判断,第二句是梅森素数猜想,前文已完成证明。第三句是瓦格斯塔夫素数猜想,证明该猜想与证明梅森素数猜想一样,分两步骤来完成。
首先是 [(2^p)+1]/3 不都是质数,不存在可通项表达的无穷素数,这个结论由素数的定义决定。假如素数可通项表达:
通过自然数 n,就可以获得素数 pn,那么通过自然数 n+1,就可以获得素数 p(n+1)。
而相邻素数之差可为任意 2n,但通项式在自变量增 1 的情况下无法获得差值 2n 偶数全集,因为通项式由定义域获得值域的每次构造部件都是有限的,否则就不是通项表达式,而一旦构造部件有限的话,再同自变量的差值增1组合,因变量就无法产生任意差值 2n,从而反证出素数无通项公式可表达。但不能因为出现反例,就得出该类素数不存在无穷性。
其次任何无穷发散且余数为 2 值域为奇数的通项表达式,都包含无穷素数。
该判定乃是朗兰兹纲领的核心,它是孪生素数、梅森素数、费马素数、欧拉素数、高斯二次互反素数、瓦格斯塔夫素数、阿廷素数的一般化推广。
所有的通项式表达都可以转换为二进制的通项式表达。这也就是为什么阿廷猜想被朗兰兹纲领作为起点进行一般化推广的原因。由孪生素数猜想、斋藤猜想以及波利尼亚克猜想获证可得知,差值 2n 的素数对有无穷组,从这个判定出发,可以得到两个重要结论:
一是差值 2n 的素数对有无穷组二是作为素数对的偶数差值可无穷大由此可推理出任何无穷发散且余数为 2,值域为奇数的通项表达式,都包含无穷素数。即:
p= f(x)+2,其中 f(x)的值域为奇数因为某通项式 f(x)的值域全部为无穷奇数;
故可得到 f(2)- f(1)、f(3)- f(2)、…、f(n)- f(n-1);
以上为素数函数通项式值域中相邻因变量的差值数列,它们的每一项都属于偶数集,假如 f(n)项为素数,f(>n)不再有素数,那么将出现以下数学矛盾。
一是 f(n+k)- f(n)的差值为 2n: 若 f(n)没有后继素数存在,相邻因变量的差值 2n 就不存在;
若 f(n)没有等差素数对存在,相邻等差素数对的无穷性就不存在。因此必有f(n+k)是素数。一旦f(n+k)是素数,那么必有f(n+k+t)- f(n+k)的差值为 2n,同样:
若 f(n+k)没有后继素数存在,相邻因变量的差值 2n 就不存在;
若 f(n+k)没有等差素数对存在,相邻等差素数对的无穷性就不存在。
因此必有 f(n+k+t)是素数。如此无限延伸,“无穷发散且余数为 2,值域为奇数的通项表达式必存在无穷素数”的判定,就可以得到证明。
由此可以看出,波利尼亚克猜想比阿廷猜想更加本质,是阿廷猜想的一般化推广,是朗兰兹纲领的核心。而波利尼亚克猜想又以孪生素数猜想为核心,不等于 2 的任何素数对差值都不是孪生素数差值,因而跟孪生素数猜想无直接关联。所谓逼近的说法,只会产生误导,因为它不能成为逻辑演绎的强势前提命题,但它不是没有意义的,它将成为归谬证明的参照系。孪生素数序与孪生素数对的迭代无漏相邻表达式乃是核心中的核心。一切数学皆由此展开。
它等价于这样一个判断:如果有两个素数可用通项式表达,那么就有无穷多个素数可用这个通项式表达。同时这个通项式也表达了无穷多个合数。这个貌似非常一般化推广的判定,实际上只是孪生素数猜想的推论,梅森素数猜想也依然是孪生素数猜想的推论。

数学家梅森
5. 二维线性空间必有二维素数基底的思想可证明梅森素数有无穷个
假如2 ^p-1>N时,N为给定的超大正整数,梅森数将不再含梅森素数,那么由2 ^p-1≠q可知,2 ^p≠q+1,即2的素数次方,不能用素数二元基底表达,据此将不难证明,2 ^p也不能用该素数二元基底的线性映射表达。这就同存在无穷个2 ^p类型数能够二元整数表达相矛盾,从而归谬证明了2 ^p-1≠q是不真的,梅森数必含梅森素数。整数二元分割必有二元素数基底的思想,在这里再次大显身手。
关于二线性空间必有二维素数基底的思想,有各种变形表达。比如2n=ap+bq,其中2n=p+q是二维素数基底表达所有偶数,2n的通项表达是(p+q)(a+b)T,其中(a+b)T是二维素数的一个线性映射,二维线性空间有很多组基底,不是唯一的,但二维素数基底是唯一的,还有特殊类的素数基底也是唯一的,(1+q)型素数基底也是唯一的,(p+1)型素数基底也是唯一的,甚至(1+1)型根素数基底也是唯一的,如果类型整数不存在根素数基底,那么类型整数便不存在,素数基底是各种类型整数通项存在的必要条件,必要条件不具备,类型整数通项便不存在。关于该命题的证明,在《数学底层引擎相邻论和重合法》一书中有多篇论文阐释过论证过,这里就不重复表达了,它是选择公理在整数领域里的体现,可与选择公理等价,只不过它在连续数学里是公理,它在离散数学里却是一个可证明的定理。证明关键用到了,伯特兰-切比雪夫定理,以及三元方程两元互素便两两互素定理以及互补偶数因互异而相邻互素定理,以此巧妙证明了,没有基底的线性映射所得到类型整数是空集,从而证明了不断递增的二维线性空间必有不断递增的二维素数基底的思想。
该思想还成功证明过考拉兹猜想。考拉兹迭代函数是: f(f(x))=(3x+1) / 2^ i(x 为奇数,i为被除数中所有 2因子的个数),首先证明3x+1必含2^k偶数,因为3x+1,3x+2,3x+3,此三类数之并集是必含2^k偶数的,而3x+1=2^k是本原解方程,其它两项都有因子与另两项的其中一项有共因子,要么有2,要么有3,故不是本原解方程,而本原解方程一旦无解,其它两项便无解,但三类方程是必有解的,故本原解方程一定有解,从而证明了,3x+1=2^k必有无限解。继而证明3xi+1,x任意首项所获得的迭代偶数集也必有2^k偶数,证法是一样,若3xi+1迭代所获得的所有整数,不含2^k偶数,那3(xi+2)+1所迭代获得的所有整数,也不含2^k偶数,而xi+2 可后继获得所有奇数,这就意味着,在所有奇数定义域下,3x+1与2^k 都是不等式,这就同前文已经证明的 3x+1 与 2^k 有交集矛盾。故可归谬得到,任意奇数生成元 x每次所迭代产生的对象集与2^k 必有交集,否则都无交集。从而证明了3x+1整数必有2^k偶数。

黄金分割律在分型几何中
6. 二维线性空间必有二维素数基底的思想可证明斐波那契素数有无穷多个
人们猜想形如1/√5{(1+√5)^n/2^n-(1-√5)^n/2^n}的斐波那契素数也有无穷多个,这类素数虽不能简单归为整系数不可约多项式类型的素数,因为它的表达是迭代解析式的,而非直接代数式的,但通过简化归约,斐波那契数具有代数式通项,不过它不是多项式、分式和根式,而是指数式。由于该指数式迭代项可转换为多项式通项,正整数变量是可数的,每次可取给定正整数,故斐波那契数二项式迭代项可归约到斐波那契数二项式及其线性映射,即b0=0,b1=1,…,bn=b(n-1)+b(n-2)(n=2,…),可变换为rb3=sb1+tb2。可得出右边具有二元素数基底,存在初项斐波那契数为素数,其线性映射的结果可得到所有的斐波那契数,其中定有斐波那契素数,因为三元方程,若不能用两元素数之和表达第三元(指偶数),便不能用两元素数的线性映射来表达第三元(此为哥猜成立的重要引理,已获证),若为奇数可添加奇素数3来实现。继续用新获得的斐波那契素数为初项,经线性映射又可得到更新的斐波那契素数,如此可不断进行下去。于是可知,斐波那契素数是无穷的。
换句话来表达就是,假如1/√5{(1+√5)^n/2^n-(1-√5)^n/2^n}>N时,N为给定的超大正整数,斐波那契数将不再含斐波那契素数,那么由1/√5{(1+√5)^n/2^n-(1-√5)^n/2^n}≠q可知,1/√5{(1+√5)^n/2^n≠q+(1-√5)^n/2^n},即2的整数倍数,不能用素数3+q的二元基底表达,据此将不难证明,2 的整数倍数也不能用该素数二元基底的线性映射表达。这就同存在无穷个2 k类型数能够二元整数表达相矛盾,从而归谬证明1/√5{(1+√5)^n/2^n-(1-√5)^n/2^n}≠q是不真的,斐波那契数必无限蕴含斐波那契素数。这里通项表达的代数式由于底数含无理数,素数基底无法直观体现。但可变换为rb3=sb1+tb2,即二维护素数基底极其线性映射可表斐波那契数,一定存在两初项斐波那契素数之和或两初项斐波那契素数之差表达的斐波那契数,否则斐波那契数便无通项表达。若素数不无限递增,通项中的斐波那契数便无法无限递增。以此便证明了,斐波那契数欲无限递增,必有斐波那契素数无限递增,因为二元素数在有限范围里进行线性映射,必产生新增素数,新增素数变大时,素因子的个数就要变少,否则左右不等,因为素数大小有限,素因子的个数有限,二元代数式必是一个有限值,所映射的素因子必越来越少,最后必剩下一个。一个不剩下不可能,那就数列变有限了,矛盾,最后还剩一个以上也不可能,因为,凡有新素数,二元代数式皆可采用,故最后必剩下一个互异的素因子,定是新增素数因子,它就是新增的斐波那契素数。
两素数之和直接是表达偶数的基底,并非直接是表达斐波那契数的基底,但可以是表达它的素数参数基底。素数参数表达式所刻画的多因子,不能无限新增,素因子只能通过变大来等值素因子的变少。两个斐波那契素数相加或相减未必都等于斐波那契数,但一定等于经线性映射而产生斐波那契数,其中必有斐波那契素数。因为斐波那契迭代函数每项都有不共素因子新增且含单个素因子的数即斐波那契素数,一旦不能,就终止继续迭代了。假如仅一个初项存在斐波那契素数,也就是说线性映射的三元数都不再含1,如此就会导致,相邻的斐波那契数之比超过2,小于1。因为含新增素数,还含其它因子,因此它是素数有限长数列且满足乘法交换律条件下的映射。
以二维素数为基底的斐波那契式线性映射,所获得的对象,不可能全都是合数。假如是,意味着大于N的斐波那契数不再含素数,即二维素数基底的线性映射不会生产新素数,等于大于N后的整数不含两素数之差的线性映射所产生的斐波那契数,肯定有很多偶数型的,这就与斋藤猜想和波利尼亚克猜想获证相矛盾,该两猜想认为,两素数之差或两素数之和是可以产生任意偶数2n的。其中每个素数加上相应的偶数2t就可产生无穷个新增素数,那2t是否蕴含2b呢?2b是初项斐波那契素数p与另一斐波那契素数q之间的差值,即(p+2)(1+b)T=aq,斐波那契奇数项都可用aq表示,其中a=1时,2b就是两斐波那契素数之间的差值,如果存在2b∈2t,则有(p+2)(1+b)T=q,根据“二维线性空间通项有无限解则二维素数基底必有无限解”的定理,可得2b=q-p,否则类型2b不存在,这就证明了,通过斐波那契素数初项p经斐波那契的线性变换(1+b)T可得到一个间隔偶数2b相加,于是可获得新增素数q1,用新增素数q1再做初项斐波那契素数,又可获得新增素数q2,如此可不断进行下去,可见没有二元素数之差表达的类型整数基底方程,就不存在斐波那契数列,而一旦有基底方程,便有了无穷个斐波那契素数。
斐波那契数列存在偶数间隔,该类型偶数,存在两素数之差表达的基底解,如果不存在,该类型偶数便不存在,但该类型偶数是可以通过aq-p来获得的,其中p、q是奇素数。方程有无限通项解就一定有无限基底解,否则通项解会成空集,无端则无类,不撒种子,不成森林。类型偶数存在两素数之差表达的基底解是证明斐波那契素数具有无穷个的核心引理。

海螺中的黄金分割律
整数二元分割必有二元素数基底的思想,在证明斐波那契素数无穷性问题上又一次大显身手了。是“二维线性空间通项有无限解则二维素数基底有无限解”和“二维素数基底无解则二维线性空间通项必无解的思想”证明了考拉兹猜想,证明了哥德巴赫猜想和孪生素数猜想,还证明了梅森素数猜想和斐波那契素数猜想。这个思想是如此的朴素,乃至“说破人须失笑”。(文/罗莫)
参考文献:
[1] 高斯 . 算术研究 [M]. 法国科学院出版社,1801.
[2] 蔡天新 . 数论从同余的观点出发 [M]. 北京:高等教育出版社,2012.
[3] 潘承洞,潘承彪 . 代数数论 [M]. 济南:山东大学出版社,2001.
[4] 罗素,怀海德 . 数学原理 [M]. 剑桥郡:剑桥大学出版社,1910.
[5] 俞晓群 . 自然数中的明珠 [M]. 上海:上海教育出版社,2013.
注释:
①梅森数是指形如 2^p-1 的正整数,其中指数 p 是素数,常记为 Mp。 若 Mp 是 素 数, 则 称 为 梅 森 素 数。p=2,3,5,7 时,Mp 都 是 素 数, 但M11=2047=23×89 不是素数,是否有无穷多个梅森素数是数论中未解决的难题之一。截至 2013 年 2 月累积发现 48 个梅森素数,最大的是 Mp=257885161-1(即2 的 57885161 次方减 1),此时 Mp 是一个 17425170 位数。
②波利尼亚克定理。波利尼亚克猜想断言,任意给定的偶数都有无穷对的素数差值与其相等。它是孪生素数猜想的一般化推广,差值为 2 的孪生素数是该定理的一个推论。实际上它和孪生猜想是等价命题,因为证明差值越小的素数对是否具有无穷性就越难,差值2是最小的,最小的差值素数对具无穷性获证,意味着差值 2n 的素数对具无穷性也获证。